Moved by Math

Applied game dev math can be tricky, but is really rewarding. Here’s a follow-up to Nevyn’s Twitter thread on his journey from incomprehensible mess to enlightened one-liner. Follow the dev journey and learn the math involved.

I studied game programming in 2004, which included linear algebra — matrices, vectors, that sort of thing. It was the most fun I’ve ever had with math, since it’s the basic underpinnings for 3D graphics, physics and many other game development topics, so I was able to immediately try out every new thing we learned in code, and literally play with it.

Fast forward sixteen years, past a long iOS career that didn’t really need that much math, to the now where I’m part of a group building the future of VR. Alloverse is 3D, and built on game tech, so all that old knowledge is needed again. I’m kind of a lazy programmer, so it’s rare that I reach a point where I truly understand something; I enjoy the building and the result more. However, in this case that wasn’t an option, and with some help from my friends and colleagues, enlightenment was reached and the satisfaction was supreme.

Failing slowly

So here’s the project, which I thought would be easy: point your hand at a thing, press the grabby button, and have the thing you’re pointing at move, its position and rotation staying fixed relative to your hand as if you glued it onto the end of a stick.

Alloverse’s front-end is Lua, but its shared code and backend is C, so I was doing this math in C and only using transformation matrices. After several days of dead-ends, I ended up writing a minimal test case in Lua on the same VR engine that Alloverse uses, Lovr. It took an entire day, but Lovr’s APIs are really stellar, and it was so much fun. You can see the result in the video at the top of the post. Here are the important bits:

function qdiff(q1, q2) -- ??? wtf, don't ask me
  return lovr.math.quat(q2) * lovr.math.quat(q1):normalize():conjugate()
end

function box:select(hand)
  self:deselect(self.heldBy)
  self.heldBy = hand
  self.offset:set(self.position - hand.to)
  local handRot = lovr.math.quat(lovr.headset.getOrientation(self.heldBy.device))
  self.rOffset:set(qdiff(handRot, self.rotation))
  self.distance = (hand.to - hand.from):length()
end

function box:update()
  if self.heldBy then
    local straightAhead = lovr.math.vec3(0, 0, -1)
    local handRotationQ = lovr.math.quat(lovr.headset.getOrientation(self.heldBy.device))
    local handRotation = lovr.math.mat4():rotate(handRotationQ)
    local pointedDirection = handRotation:mul(straightAhead)
    local distantPoint = lovr.math.newVec3(pointedDirection):mul(self.distance):add(self.heldBy.from)
    self.position:set(distantPoint + self.offset)
    self.rotation:set(lovr.math.quat(self.rOffset) * handRotationQ)
  end
end

You don’t have to understand this code, that’s how wrong it is. My general thinking was:

1. Find the point on the grabbed box which should stay fixed relative to the hand. Save the offset from the box’s origin to that point. Also save how far away it is.
2. Calculate the box’ new position by taking the hand’s new position, adding the distance away from the hand, and adding the offset (from grabbed point to origin on the box).
3. Try to do the same thing for rotation by saving the difference in rotation between the hand and the box, and set the box’ new rotation to the hand’s rotation plus the saved difference.

I figured it’d be easier to decompose the problem from matrices (which I know how to work with and are okay proficient with, but which are hard and always do my head in) to positions and rotations (positions are easy, but for rotations I haven’t used quaternions before, so it’s all new territory for me).

The problem was, as you can see in the video above, that the rotation was applied in the wrong coordinate system, so it rotated along X when I wanted to rotate around Z, and so on, depending on the camera location when drag started. This is something I conceptually understand how to fix when working with matrices (you usually need to invert the order of multiplication, since matrix multiplication is not commutative), but with Quats I’m lost.

Enter: frustration. All that work to switch tools, only to want to switch back, and I didn’t understand anything any better. I had spent over a week full-time on this already (to the point where it would distract me from eating and sleeping outside of work hours).

A little help from my friends

It was time to ask for help. Luckily, I had the privilege to befriend math prodigy and VR hacker Rasmus when I lived in San Francisco. When I described the problem over Messenger, he disappeared for a few minutes and then returned with a PDF with some LaTeX formulas. 🤯🤯🤯

Apparently, my thinking that I needed to keep track of the point at which the “stick” was touching the box muddled the waters for me, making the problem much more complex than it had to be. All I really needed was to save a single transform — “HandFromBox” above — and everything just falls into place!

Still, I was not able to take this theory and apply it to practice on my own. Luckily again, I’m now colleagues with one of my closest friends (who also studied Game Programming at BTH with me): Voxar! We spent two whole afternoons pair programming using the amazing screen sharing tool screen.so. The result is beautiful: 19 lines replaced with 4.

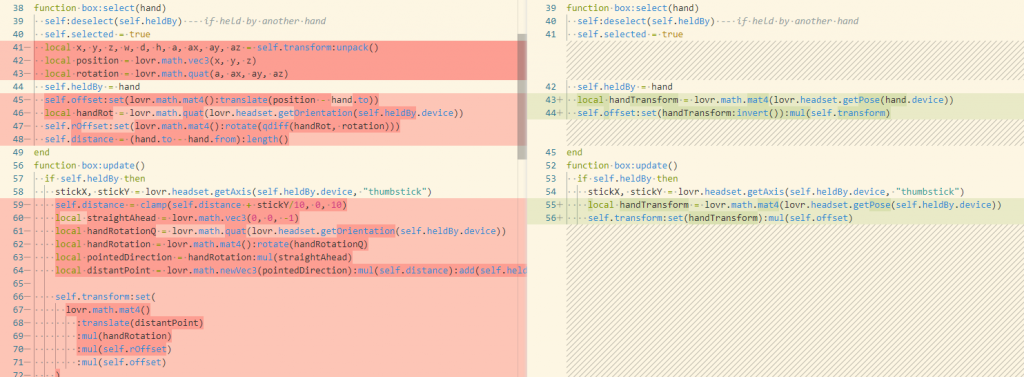
Plus, you know, it works 😅😂

Voxar and I are both working on our collaboration style (at one point, I argued vehemently for a full hour that he was wrong, but of course he was right 😅). We had two big squabbles; but since they were such sticking points for us that we kept arguing our sides vehemently, we ended up teaching ourselves something really valuable when working with matrices. Rasmus’ chosen terminology — “XFromY” — really did our heads in for the longest while, but using it means that the naming itself helps you understand the semantics of matrix multiplication. Again, since matrix multiplication isn’t commutative, this is super valuable. In the past, I would just swap every multiply in my code until it works; but after this exercise, I’m actually able to reason about the order and figure out the correct order without experimenting. This has the advantage that I don’t introduce two mistakes that cancel each other out; I’ve done this mistake many times, and leads to just writing tons of bad math that all breaks once you fix one load-bearing bug somewhere.

For example, if you have a transform that represents the position, rotation and scale of your box in the world coordinate space (i e relative to the origin point of the world at 0,0,0), you can call it WorldFromBox. We can multiply a point that is relative to box with this, and get a point that is relative to world — i e it is a transform from the ‘box’ coordinate system to the ‘world’ coordinate system.

So say we want handFromBox to get that “offset” we talked about before, converting from the hand’s coordinate space to the box’ coordinate space. We have the hand and the box transformation matrices (representing their position, rotation and scale in a single big box of numbers) called worldFromHand and worldFromBox. We can get handFromWorld by just invert()ing worldFromHand. Thus,

local handFromWorld = worldFromHand:invert()
local handFromBox = handFromWorld * worldFromBox

Notice how the two “world”s line up, making the line readable! This was a big revelation for me.

With code and understanding in place, we ran our virtual victory lap! (I accidentally only recorded Voxar’s mic, not my own)

It gets tricker

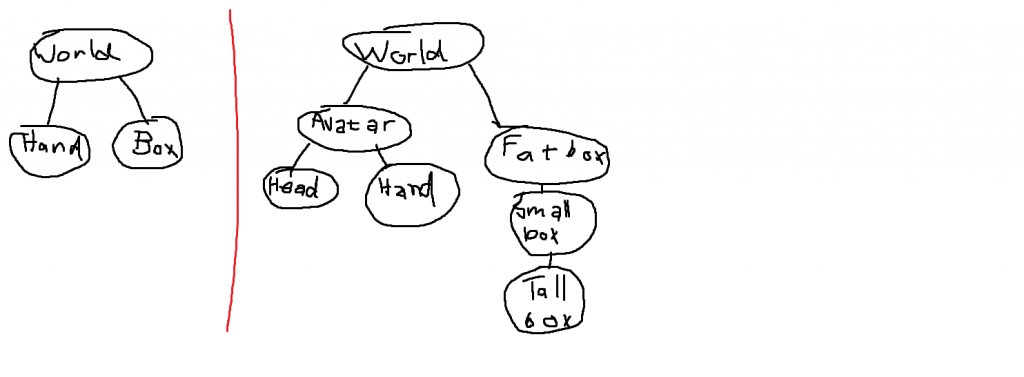
We weren’t quite ready to port it back to Alloverse though, because Alloverse is a scene graph. You know, like on a regular 2D computer: you have a window, and the window has a text field and a button. When you move the window, the button follows the exact movement of the window, keeping its relative position to the title bar. It’s the same thing on web sites. It’s really hard to build user interfaces without a scene graph.

You really got to keep things straight with a scene graph. It’s really easy to write math that seems to work, but where you ended up accidentally assuming that one tiny part of the equation is in world coordinates when it isn’t. For example, in my prototype, the hand belongs to the world (see left); but in Alloverse, the hand belongs to the avatar which belongs to the world (see right). Also, the thing you’re moving might belong to a parent object, rather than being in the world.

Getting a matrix that represents WorldFromTallBox is easy: just recursively multiply tall box’ transform with each of its parent nodes in turn.

function Box:transformInWorld()
  if self.parent then
    return self.parent:transformInWorld() * self.transform
  else
    return self.transform
  end
end

Converting from any arbitrary node to any arbitrary node is trickier, but again, Rasmus’ nomenclature helped us out. I’m sure there are more efficient solutions, but this works:

function convert(m, a, b)
  local worldFromA = a:transformInWorld(
  local worldFromB = b:transformInWorld()
  local bFromWorld = worldFromB:invert()
  local bFromA = bFromWorld * worldFromA
  return bFromA * m
end

This is taken from the same source linked before, but a few commits later.

And hey presto, that took about a DAY of flailing around in C and an HOUR in Lua.

A bad case of the typos

Okay! The prototype works! Let’s just port the math over to C and we’re done! …

Well. We ported the math over line-by-line. It refused to work. Things would just fly off the screen from a simple hand movement, some matrix clearly being multiplied in the wrong order. We debugged for an entire day, making really really really sure every single detail was correct. When we had read the code so many times we knew the fault must lie otherwhere… we looked at my home baked matrix class. … and of course, my multiply_matrix method had a typo, swapping the arguments. So, every single multiplication in the entire project so far had been written in the incorrect order to compensate for this load bearing bug.

With absolute zero trust remaining in my skill to copy-paste math from StackOverflow, we moved to felseva’s mathc library, which has all the linear algebra you need for 3D graphics, physics and all that jazz, and nothing less, and nothing more. It’s just lovely. (Its API is very similar to Cirno’s Perfect Math Library, which clearly is just perfect.)

This of course broke everything else, so I had to invert every single multiplication in the project before moving on …

http://gph.is/YBEhf4

At long last…

Yes. What you’re looking at is me moving the jukebox app with the grabby button. And it moves. Exactly following the hand’s movement and rotation. IT’S PERFECT! IT’S BEAUTIFUL! IT’S TWELVE LINES OF CODE!

On the one hand… I feel like such a fraud. I like watching Twitch streams of other game devs, and I feel like this is the sort of thing they’d go like “oh, and then we need to be able to move things, lemme just” and five minutes later it’s there. For me, it was several full days of work a few months ago before we were incorporated and I was working in my free time; and now followed by two additional full weeks of work.

On the other hand, I’ve only been on this job full time a single month now, and I’ve learned so very very very much so far. This is just one of the frankly quite amazing things we’ve accomplished in this short time, and there’s much more to come.

---

In conclusion:

• Using the XFromY naming convention for matrices is really handy.
• Understanding your code can be better than just writing something that seems to work. Figure out when that’s the case and spend the time to get there.
• Lovr‘s just great.
• Maybe don’t write your own math primitives unless you really know what you’re doing or you can’t avoid it.
• You can check out our sample code on GitHub.
• Actually, you can check out our product’s final state on GitHub too (warning: C), because Alloverse is Open Source!

If you enjoyed this post, do follow @alloverse on Twitter (or just @nevyn, @voxar, @rasasmus) to get notified of new posts, or maybe even come join us on Discord? 🤗